Introduzione al Significato dei Solidi Platonici
Le nozioni relative al significato dei Solidi Platonici ci pervengono dalla cultura greca.
I Solidi Platonici devono il loro nome alla descrizione che nel dialogo “Timeo” ne fa Platone (vissuto tra il 428 e il 327 a.C.).
Caposaldo della cultura occidentale di ogni epoca, l’opera di Platone diviene paradigmatica anche in questo caso determinando la fortuna di queste particolari figure geometriche che assumono il nome del loro “divulgatore”.
Platone infatti non fu il primo a occuparsi di queste figure geometriche, benché ne abbia dato un’interpretazione speciale.
I loro primi studiosi furono i Pitagorici e, in seguito e in maniera più sistematica, Teeteto, contemporaneo dello stesso Platone.
I Solidi Platonici vengono chiamati anche Poliedri Regolari, soprattutto in ambito matematico, oppure, specialmente quando gli autori si rifanno all’antichità, Figure Cosmiche.
Essi sono soltanto cinque, ovvero:
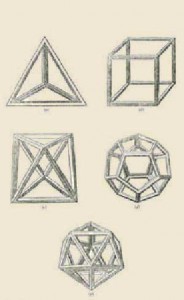
Il Tetraedro
Viene detto anche Piramide a base triangolare ed è formato da Quattro Triangoli Equilateri.
L’Esaedro
E’ chiamato anche Cubo ed è formato da Sei Quadrati.
L’Ottaedro
E’ formato da Otto Triangoli Equilateri.
Il Dodecaedro
E’ costituito da Dodici Pentagoni.
L’Icosaedro
E’ formato da Venti Triangoli Equilateri.
Proprietà e peculiarità dei Solidi Platonici
I Solidi Platonici sono gli unici Poliedri Convessi che presentano tutte le seguenti proprietà.
Sono gli unici solidi le cui Facce sono equilatere e uguali tra loro, ovvero congruenti, e i cui Spigoli e i cui Vertici sono equivalenti.
Sono le uniche figure solide che, inscrivendosi in una Sfera, presentano tutti i loro vertici giacenti sulla superficie della stessa.
Questa loro Perfetta Simmetria permette alcune peculiarità.
Il Tetraedro, che presenta 6 Spigoli, 4 Facce e 4 Vertici, si auto riproduce all’infinito quando si congiungono tra loro i Centri delle sue facce.
L’Esaedro e l’Ottaedro hanno entrambi 12 Spigoli e il numero di Facce e di Vertici invertiti (l’Esaedro ha 6 Facce e 8 Vertici, mentre l’Ottaedro ha 8 Facce e 6 Vertici).
Congiungendo i Centri delle Facce dell’Esaedro si ottiene un Ottaedro e viceversa.
Il Dodecaedro e l’Icosaedro hanno entrambi 30 Spigoli e il numero di Facce e di Vertici invertiti (il Dodecaedro ha 12 Facce e 20 Vertici, mentre l’Icosaedro ha 20 Facce e 12 Vertici).
Congiungendo i Centri delle Facce del Dodecaedro si ottiene un Icosaedro e viceversa.
Il Dodecaedro e l’Icosaedro presentano un forte legame con il Rapporto Aureo (rappresentato dalla lettera greca “phi”) poiché tramite esso è possibile calcolare le loro aree e i loro volumi e il rapporto delle lunghezze dei loro spigoli.
I 12 Vertici dell’Icosaedro si possono dividere in 3 Tetradi i cui Vertici corrispondono agli Angoli di 3 Rettangoli Aurei perpendicolari tra di loro e aventi un solo Punto in comune, corrispondente al Centro dell’Icosaedro.
I Centri delle 12 Facce del Dodecaedro si possono dividere in 4 Tetradi, ciascuna corrispondente ai Vertici di un Rettangolo Aureo.
Dimostrazione dell’Esistenza dei Cinque Solidi Platonici
La dimostrazione che esistono solo questi Cinque Solidi Platonici venne data diverso tempo dopo la loro scoperta.
Essa si basa sul fatto che solo il Triangolo Equilatero, il Quadrato e il Pentagono regolare possono essere Facce di Poliedri Regolari.
Ciò è dovuto al fatto che in ogni Vertice di un Poliedro Regolare devono convergere almeno 3 Facce che non stiano sullo stesso piano, e quindi la somma dei loro angoli deve essere inferiore a 360°.
Un’ulteriore dimostrazione dell’esistenza di soli Cinque Solidi Platonici fa uso della Relazione di Eulero: V+F-S=2 (dove V è il numero dei Vertici, F il numero delle Facce e S il numero degli Spigoli).
La Storia del Significato dei Solidi Platonici continua nelle seguenti pagine:
I Solidi Platonici da Pitagora a Euclide
